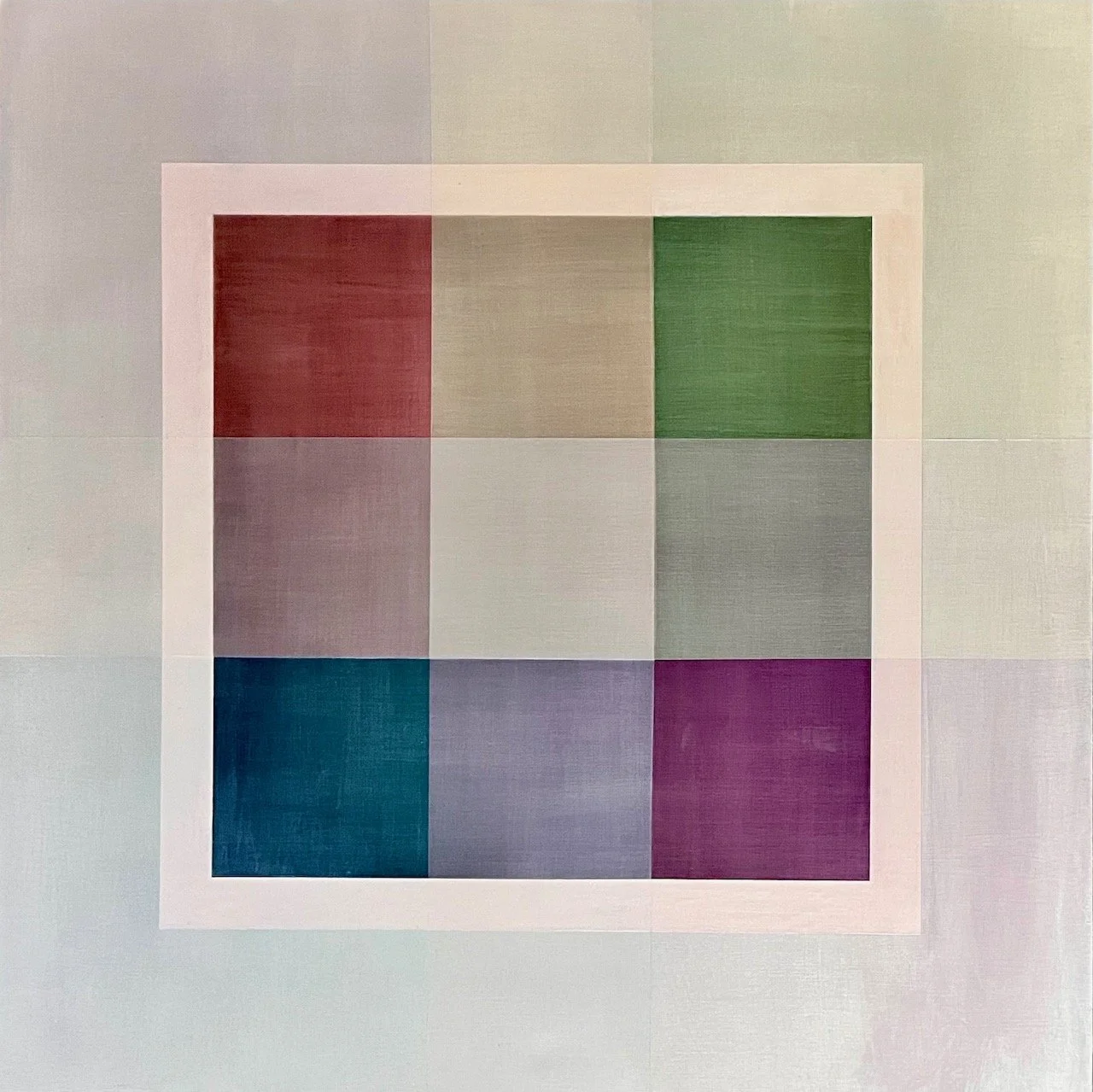Flatland
The paintings in Flatland explore geometric projections of 4-dimensional cubes onto flat wooden panels, using acrylic paint and multi-chrome pigments. Flatland serves as a metaphor for our desires and attempts to understand the inexplicable—complicated facets of problems without attainable solutions—in the specific case, due to our perceptual limitation to 3 dimensions—but also in other cases, such as our inability to understand people who think radically differently from us.
Metaphorically, this series pays homage to “Flatland”, the novella written by Edwin Abbott in 1884, which was probably the first sci-fi literature I read as a kid; it made an outsized lasting impression on me. The book is centered around a flat protagonist who is visited by sphere from the 3-dimensional world. The first part of the book sets up the societal hierarchy of Flatland, which serves as a parable of the randomness of being born into a certain gender or societal class, along with the limits and privileges associated with those attributes. When visited by the sphere, the protagonist comes to realize that there is more in the universe than he is able to perceive. When he brings this message back to the people of Flatland, he is labeled a heretic. Another lovely aspect of the book is that the visual description is essentially the basis of calculus—the building and dissecting of n-dimensional objects using planes, which is essentially the reverse of what these paintings are doing: compressing 4-dimensional cubes into 2 (and slightly more than 2) dimensions.
Finally, Flatland is also a nod to the current rampant dissemination of mis-information, embodied by the resurgence of the Flat Earth movement.
With this body of work, I pay tribute to our ongoing attempts to understand the indescribable, both through mathematical and scientific exploration, as well as through personal attempts to understand those with different viewpoints, in order to bridge the growing political divide in our country.
CEL 2023
[NOTE: click on each image for multiple views and effects of different illumination]